In Laplace transforms of continuous time signals, we have the s plane. In the ztransform of discrete time signals, there is the unit circle. In time scales, both are special cases of the Hilger circle shown here.
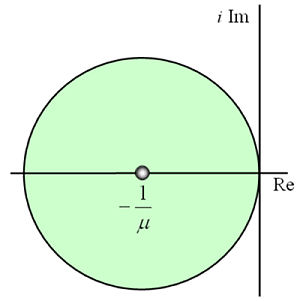
The Hilger circle hass a diameter equal to the reciprical of graininess and is tangent to the imaginary axis.
For discrete time, the graininess is one. The unit circle in the z domain is centered about the origin. Why is the Hilger circle tangent to the imaginary axis and not centered? The answer is that traditional discrete time equations are of the form
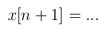
Time scale equations for discrete time, on the other hand, are of the form
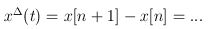
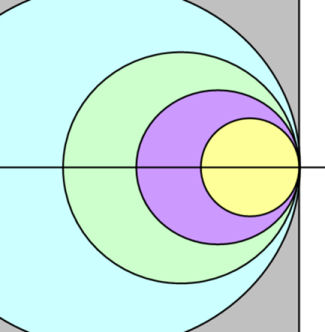
As the graininess decreases, the Hilger circle becomes larger. When the graininess is one, we have the unit circle denoting the region of stability for discrete time. As the graininess goes to zero the time scale approaches continuous time. The circle grows to fill the entire left half plane corresponding to the left half plane of stability in the s domain for continuous time. In the picture below, this is shown in grey
For positive graininess, the Hilger complex numbers, the Hilger real axis, the Hilger alternating axis, and the Hilger imaginary circle (or simply the Hilger circle) are all respectively defined as
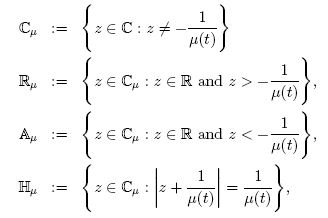
and, for zero graininess,
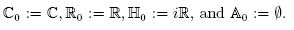
For any
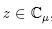
the Hilger real part of z is
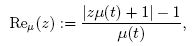
and the Hilger imaginary part is
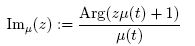 . .
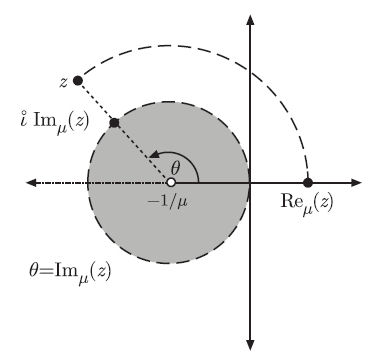
The Hilger Complex Plane.
Over the interval
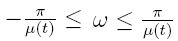
the Hilger pure imaginary number
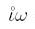
is
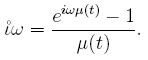
For zero graininess,
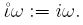
|